Hiển thị các bài đăng có nhãn Toán Cấp 2. Hiển thị tất cả bài đăng
Hiển thị các bài đăng có nhãn Toán Cấp 2. Hiển thị tất cả bài đăng
Chủ Nhật, 7 tháng 8, 2016
Thứ Năm, 18 tháng 6, 2015
Để học tốt hình học 9
Download: Để học tốt hình học 9
Trong khi chờ 123doc duyệt tài liệu, mời các bạn xem trước 20 trang đầu:
Chủ Nhật, 5 tháng 4, 2015
Thứ Năm, 2 tháng 4, 2015
Đường thẳng Simson, Đường thẳng Steiner
1. Định lý về Đường thẳng Simson
Cho tam giác nội tiếp trong đường tròn tâm
nội tiếp trong đường tròn tâm 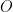 . Gỉa sử
. Gỉa sử  là một điểm nằm trên
là một điểm nằm trên 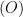 sao cho
sao cho  không trùng với ba đỉnh của tam giác. Khi đó hình chiều vuông góc
không trùng với ba đỉnh của tam giác. Khi đó hình chiều vuông góc  của
của  lần lượt trên
lần lượt trên 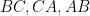 cùng nằm trên một đường thẳng. (Đường thẳng này gọi là đường thẳng
cùng nằm trên một đường thẳng. (Đường thẳng này gọi là đường thẳng 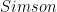 của điểm
của điểm  đối với tam giác
đối với tam giác  )
)
Chứng minh :
Ta có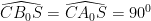 , suy ra tứ giác
, suy ra tứ giác 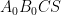 nội tiếp, suy ra
nội tiếp, suy ra  . Mặt khác vì
. Mặt khác vì 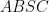 nội tiếp nên
nội tiếp nên  .
.
Nhưng vì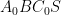 là tứ giác nội tiếp (
là tứ giác nội tiếp (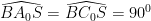 ) nên
) nên  .
.
Vậy cùng thuộc một đường thẳng.
cùng thuộc một đường thẳng.
2. Định lí về đường thẳng Steiner :
Cho tam giác nội tiếp đường tròn tâm
nội tiếp đường tròn tâm 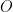 , điểm
, điểm  bất kì thuộc đường tròn sao cho
bất kì thuộc đường tròn sao cho  không trùng với các đỉnh của tam giác. Gọi
không trùng với các đỉnh của tam giác. Gọi 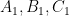 lần lượt là điểm đối xứng với
lần lượt là điểm đối xứng với  qua các đường thẳng
qua các đường thẳng 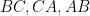 . Khi đó ba điểm
. Khi đó ba điểm 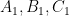 và trực tâm
và trực tâm  của tam giác
của tam giác  cùng nằm trên một đường thẳng (Đường thẳng này là đường thẳng
cùng nằm trên một đường thẳng (Đường thẳng này là đường thẳng 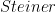 của điểm
của điểm  đối với tam giác
đối với tam giác  .
.
Chứng minh:
Dễ dàng thấy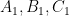 cùng nằm trên một đường thẳng song song với đường thẳng
cùng nằm trên một đường thẳng song song với đường thẳng 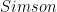 của điểm
của điểm  đối với tam giác
đối với tam giác  .
.
Ta có mà
mà 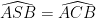 nên
nên  , suy ra
, suy ra 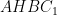 là tứ giác nội tiếp.
là tứ giác nội tiếp.
Từ đó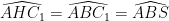
Hoàn toàn tương tự, tứ giác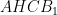 nội tiếp nên
nội tiếp nên 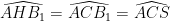
Lại có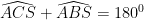 (tứ giác
(tứ giác 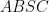 nội tiếp)
nội tiếp)
Do đó , suy ra
, suy ra 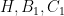 thẳng hàng.
thẳng hàng.
Vậy : cùng thuộc một đường thẳng.
cùng thuộc một đường thẳng.
Cho tam giác
Chứng minh :
Ta có
Nhưng vì
Vậy
2. Định lí về đường thẳng Steiner :
Cho tam giác
Chứng minh:
Dễ dàng thấy
Ta có
Từ đó
Hoàn toàn tương tự, tứ giác
Lại có
Do đó
Vậy :
Đăng ký:
Bài đăng (Atom)




.png)


